Multi-target Scoring (scoring)¶
Multi-target classifiers predict values for multiple target classes. They can be used with standard testing procedures (e.g. cross_validation), but require special scoring functions to compute a single score from the obtained ExperimentResults. Since different targets can vary in importance depending on the experiment, some methods have options to indicate this e.g. through weights or customized distance functions. These can also be used for normalization in case target values do not have the same scales.
- Orange.multitarget.scoring.mt_flattened_score(res, score)¶
Flatten (concatenate into a single list) the predictions of multiple targets and compute a single-target score.
Parameters: score – Single-target scoring method.
- Orange.multitarget.scoring.mt_average_score(res, score, weights=None)¶
Compute individual scores for each target and return the (weighted) average.
One method can be used to compute scores for all targets or a list of scoring methods can be passed to use different methods for different targets. In the latter case, care has to be taken if the ranges of scoring methods differ. For example, when the first target is scored from -1 to 1 (1 best) and the second from 0 to 1 (0 best), using weights=[0.5,-1] would scale both to a span of 1, and invert the second so that higher scores are better.
Parameters: - score – Single-target scoring method or a list of such methods (one for each target).
- weights – List of real weights, one for each target, for a weighted average.
The whole procedure of evaluating multi-target methods and computing the scores (RMSE errors) is shown in the following example (mt-evaluate.py). Because we consider the first target to be more important and the last not so much we will indicate this using appropriate weights.
import Orange
data = Orange.data.Table('multitarget-synthetic')
majority = Orange.multitarget.binary.BinaryRelevanceLearner( \
learner=Orange.classification.majority.MajorityLearner(), name='Majority')
tree = Orange.multitarget.tree.ClusteringTreeLearner(min_MSE=1e-10, min_instances=3, name='Clust Tree')
pls = Orange.multitarget.pls.PLSRegressionLearner(name='PLS')
earth = Orange.multitarget.earth.EarthLearner(name='Earth')
learners = [majority, tree, pls, earth]
res = Orange.evaluation.testing.cross_validation(learners, data)
rmse = Orange.evaluation.scoring.RMSE
scores = Orange.multitarget.scoring.mt_average_score(
res, rmse, weights=[5,2,2,1])
print 'Weighted RMSE scores:'
print '\n'.join('%12s\t%.4f' % r for r in zip(res.classifier_names, scores))
Which outputs:
Weighted RMSE scores:
Majority 0.8228
Clust Tree 0.4528
PLS 0.3021
Earth 0.2880
Two more accuracy measures based on the article by Zaragoza et al._[1]; applicable to discrete classes:
Global accuracy (accuracy per example) over d-dimensional class variable:
- Orange.multitarget.scoring.mt_global_accuracy(res)¶
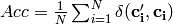
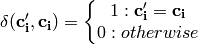
Mean accuracy (accuracy per class or per label) over d class variables:
- Orange.multitarget.scoring.mt_mean_accuracy(res)¶
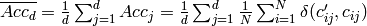
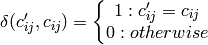
References¶
| [1] | Zaragoza, J.H., Sucar, L.E., Morales, E.F.,Bielza, C., Larranaga, P. (2011). ‘Bayesian Chain Classifiers for Multidimensional Classification’, Proc. of the International Joint Conference on Artificial Intelligence (IJCAI-2011), pp:2192-2197. |
Examples¶
import Orange
data = Orange.data.Table('multitarget:bridges.tab')
cl1 = Orange.multitarget.binary.BinaryRelevanceLearner( \
learner = Orange.classification.majority.MajorityLearner, name="Majority")
cl2 = Orange.multitarget.tree.ClusteringTreeLearner(name="CTree")
learners = [cl1,cl2]
results = Orange.evaluation.testing.cross_validation(learners, data)
print "%18s %7s %6s %10s %8s %8s" % \
("Learner ", "LogLoss", "Brier", "Inf. Score", "Mean Acc", "Glob Acc")
for i in range(len(learners)):
print "%18s %1.4f %1.4f %+2.4f %1.4f %1.4f" % (learners[i].name,
# Calculate average logloss
Orange.multitarget.scoring.mt_average_score(results, \
Orange.evaluation.scoring.logloss)[i],
# Calculate average Brier score
Orange.multitarget.scoring.mt_average_score(results, \
Orange.evaluation.scoring.Brier_score)[i],
# Calculate average Information Score
Orange.multitarget.scoring.mt_average_score(results, \
Orange.evaluation.scoring.IS)[i],
# Calculate mean accuracy
Orange.multitarget.scoring.mt_mean_accuracy(results)[i],
# Calculate global accuracy
Orange.multitarget.scoring.mt_global_accuracy(results)[i])